This is the second blogpost of Triton tutorial series.
In this tutorial, we will write a fused softmax kernel, then demonstrate how to debug the kernel with imperative way. At last, we show you how to benchmark the kernel performance.
Table of Contents
Open Table of Contents
Memory-bound Regime
In the last tutorial, we demonstrated an element-wise addition kernel, which is educationally valuable. In this tutorial, we will show you another practical case - a numerically stabilized softmax operation commonly used in deep learning models.
Naive Implement
Before diving into the Triton implementation, let’s examine a naive Pytorch version, and figure out the issue with it:
@torch.jit.script
def naive_softmax(x):
"""Compute row-wise softmax of X using native pytorch
We subtract the maximum element in order to avoid overflows. Softmax is invariant to
this shift.
"""
# read MN elements ; write M elements
x_max = x.max(dim=1)[0]
# read MN + M elements ; write MN elements
z = x - x_max[:, None]
# read MN elements ; write MN elements
numerator = torch.exp(z)
# read MN elements ; write M elements
denominator = numerator.sum(dim=1)
# read MN + M elements ; write MN elements
ret = numerator / denominator[:, None]
# in total: read 5MN + 2M elements ; wrote 3MN + 2M elements
return retIn this naive version, computing y=naive_softmax(x) for requires reading 5MN + 2M elements from DRAM and writing back 3MN + 2M elements. This is very wasteful for memory bandwidth since we’re spending all our time moving data rather than computing.
Here is an illustration from Horace He’s blog showing this case.
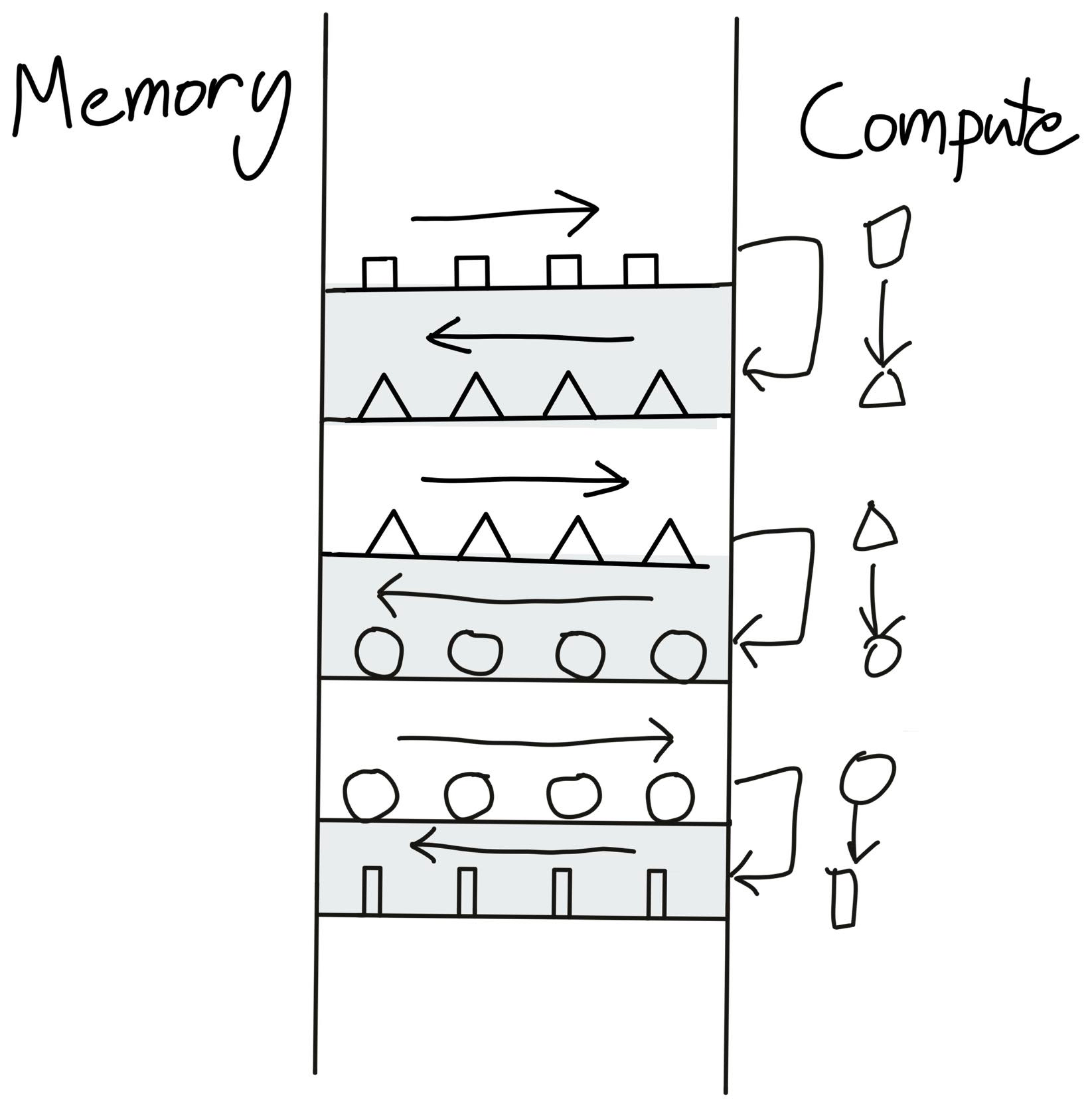
We’d prefer a custom “fused” kernel that only reads X once, does all computations on-chip, then writes back once. This would only require reading MN elements and writing MN elements, so we could expect a theoretical speedup of ~4x (i.e. (8MN + 4M)/2MN). The following figure illustrates this ideal case:
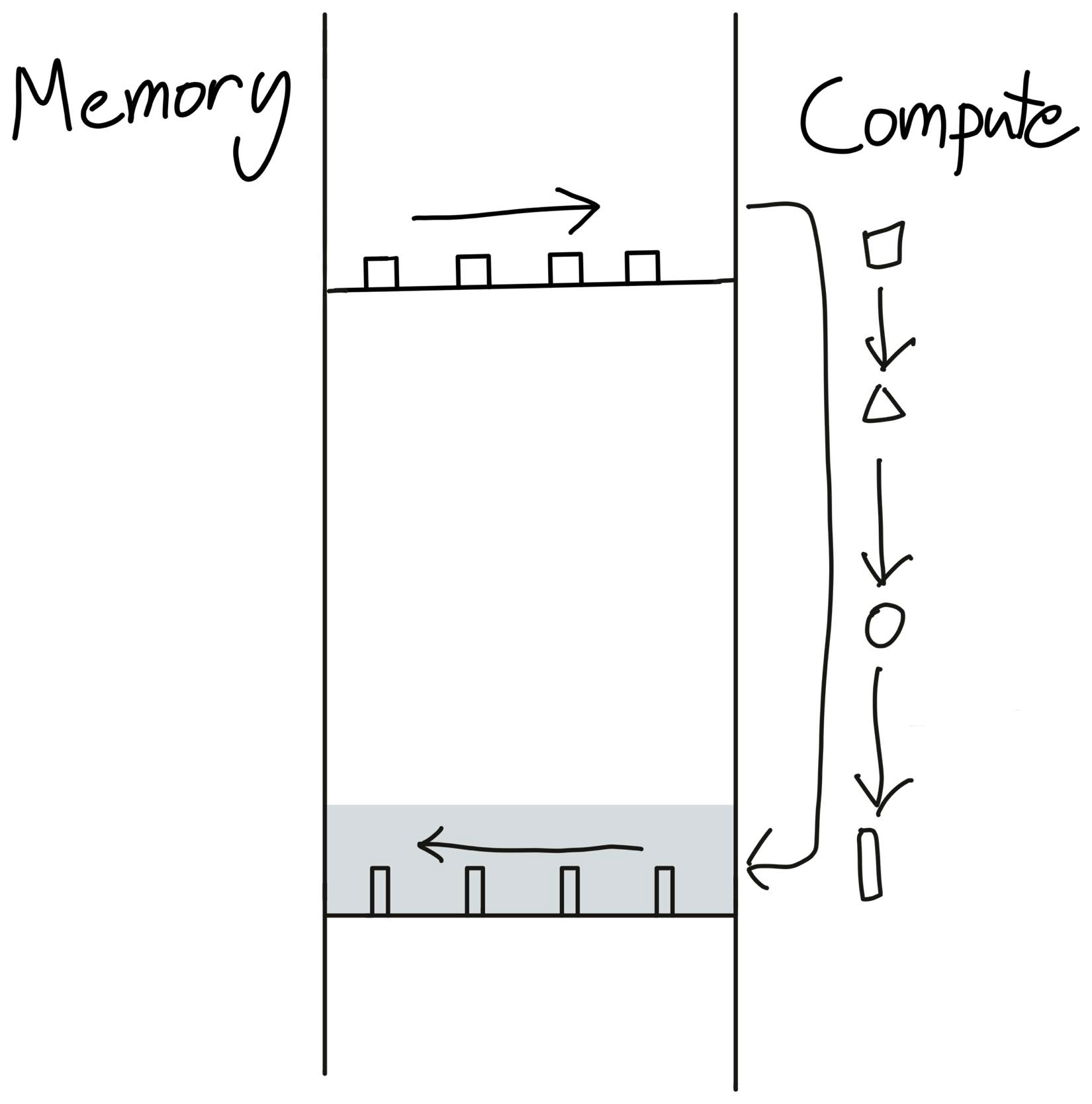
In theory, the torch.jit.script flag aims to perform this “kernel fusion” automatically, but as we’ll see when profiling later, it is still far from ideal.
Fused Softmax
Recalled that kernel will launch multiple programs, and we can let each program loads a row of the input matrix X, normalizes it and writes back the result to the output Y.
Notice that one important limitation of Triton is that each block must have a power-of-two number of elements. So we need to internally “pad” each row and guard the memory operations properly.
Here is the Triton fused softmax kernel implementation:
@triton.jit
def fused_softmax_kernel(input_ptr, output_ptr, input_row_stride, n_cols, BLOCK_SIZE: tl.constexpr):
# The rows of the softmax are independent, so we parallelize across those
row_idx = tl.program_id(axis=0)
# The stride represents how much we need to increase the pointer to next row
row_start_ptr = input_ptr + row_idx * input_row_stride
col_offsets = tl.arange(0, BLOCK_SIZE)
row_input_ptr = row_start_ptr + col_offsets
# Load the row into SRAM, using a mask to handle boundary conditions
row_input = tl.load(row_input_ptr, mask=col_offsets < n_cols, other=-float("inf"))
row_minus_max = row_input - tl.max(row_input, axis=0)
numerator = tl.exp(row_minus_max)
denominator = tl.sum(numerator, axis=0)
softmax_output = numerator / denominator
# Write back output to DRAM
output_row_start_ptr = output_ptr + row_idx * input_row_stride
output_ptrs = output_row_start_ptr + col_offsets
tl.store(output_ptrs, softmax_output, mask=col_offsets < n_cols)input_ptr + row_idx * input_row_stride move data pointer to the data block of each instance. col_offsets can cover all columns in each row, but need to consider the boundary by comparing with n_cols. After computing, seek the output data pointer in each instance, and write back to DRAM using tl.store.
We still need to declare a function to execute the kernel, and it’s very simple.
def softmax(x: torch.Tensor):
n_rows, n_cols = x.shape
BLOCK_SIZE = triton.next_power_of_2(n_cols)
num_warps = 4
if BLOCK_SIZE >= 2048:
num_warps = 8
if BLOCK_SIZE >= 4096:
num_warps = 16
grid = lambda meta: (n_rows, )
output = torch.empty_like(x)
fused_softmax_kernel[grid](x, output, x.stride(0), n_cols, BLOCK_SIZE=BLOCK_SIZE, num_warps=num_warps)
return outputAnother optimization technique involves increasing the number of threads in each block that operate on each row. This can be achieved by increasing the number of warps (num_warp). A warp is essentially a group of threads that can execute simultaneously. If not specified, each block will default to using only one thread to process the data.
Imperative Debug
With Triton, you can write kernels using Python instead of CUDA. This approach is imperative, which naturally leads to the question: Can you debug the kernel in an imperative manner as well?
The answer is yes, and here’s how to debug a kernel in Triton.
You might think that adding ipdb.set_trace() within the kernel function would pause execution at that point. However, doing so results in the following error:
from ipdb import set_trace; set_trace() # lxylog
^
unsupported AST node type: ImportFromThis occurs because Triton uses Abstract Syntax Trees (AST) to parse Python code, and not all Python packages can be captured in this manner. Therefore, the default approach won’t work.
However, there’s a workaround. We use the @triton.jit decorator for the kernel function, and this decorator accepts arguments that enable specific functionalities. For instance, you can pass interpret=True to execute the kernel in an interpreted manner.
By doing so, you can debug the kernel just like you would with standard Python code. But notice, all objects in the kernel are wrapped by Triton as wrapper tensors. For example, you can print intermediate results as shown below:
print(row_idx)
wrapped_tensor([1384], device='cuda:0', dtype=torch.int32)
print(row_input)
wrapped_tensor([-1.0878, 0.7532, -1.0484, ..., -inf, -inf, -inf],
device='cuda:0')
print(row_start_ptr)
wrapped_tensor([140340844592712], device='cuda:0')But notice, all objects in kernel are wrapped by Triton as wrapper tensor.
Since the kernel launches multiple blocks in parallel, hitting a breakpoint will pause execution in a random block. This means that running the code multiple times may yield different results. For example, in a second run, the row_idx might differ from the first run.
However, this is not a concern because Triton operates on a Single Instruction, Multiple Data (SIMD) execution model. You can effectively debug results in any block.
Benchmark
Writing a kernel is just the first step; profiling its performance is crucial for subsequent optimization. Triton provides built-in utilities that allow us to efficiently plot the performance of our custom operations across different problem sizes.
First, let’s create a benchmark function as follows:
def benchmark(M, N, provider):
x = torch.randn(M, N, device='cuda', dtype=torch.float32)
quantiles = [0.5, 0.2, 0.8]
if provider == 'torch-native':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1), quantiles=quantiles)
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: softmax(x), quantiles=quantiles)
if provider == 'torch-jit':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: naive_softmax(x), quantiles=quantiles)
gbps = lambda ms: 2 * x.nelement() * x.element_size() * 1e-9 / (ms * 1e-3)
return gbps(ms), gbps(max_ms), gbps(min_ms)This function constructs input tensors and then invokes different kernel functions based on the provider argument to measure their running times.
Next, we’ll use Triton’s built-in benchmark decorator, triton.testing.perf_report, as shown below:
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'], # argument names to use as an x-axis for the plot
x_vals=[
128 * i for i in range(2, 100)
], # different possible values for `x_name`
line_arg='provider', # argument name whose value corresponds to a different line in the plot
line_vals=[
'triton',
'torch-native',
'torch-jit',
], # possible values for `line_arg``
line_names=[
"Triton",
"Torch (native)",
"Torch (jit)",
], # label name for the lines
styles=[('blue', '-'), ('green', '-'), ('green', '--')], # line styles
ylabel="GB/s", # label name for the y-axis
plot_name="softmax-performance", # name for the plot. Used also as a file name for saving the plot.
args={'M': 4096}, # values for function arguments not in `x_names` and `y_name`
)
)Here, x_names specifies the argument names to use as the x-axis for the plot, and line_arg identifies the argument name for different lines in the plot. We use args={'M': 4096} for the remaining function arguments. The remaining decorator configurations are primarily related to plot styles.
To run the benchmark, execute the following code:
benchmark.run(show_plots=True, print_data=True, save_path='softmax-performance')The results and plot will be generated as follows:
softmax-performance:
N Triton Torch (native) Torch (jit)
0 256.0 585.142849 630.153853 221.405396
1 384.0 646.736871 682.666643 227.555555
2 512.0 712.347810 682.666643 237.449270
3 640.0 731.428561 706.206879 235.402298
4 768.0 768.000002 722.823517 238.601945
.. ... ... ... ...
93 12160.0 833.233395 436.233193 283.615167
94 12288.0 833.084721 436.421757 283.296835
95 12416.0 832.939214 436.606592 282.985759
96 12544.0 832.796675 436.313034 283.280177
97 12672.0 832.657064 436.025816 283.371078
[98 rows x 4 columns]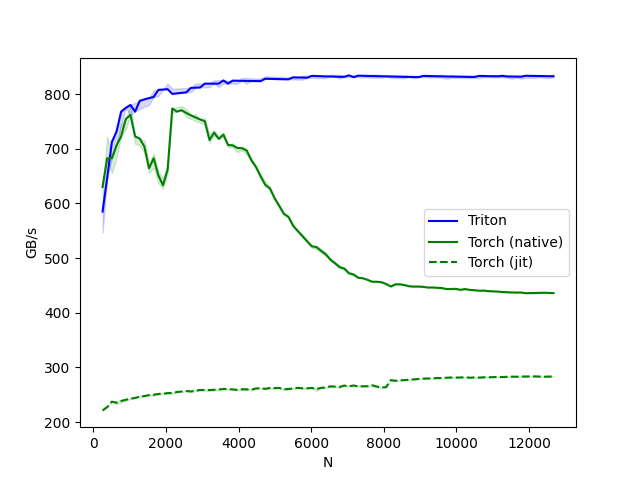
In the plot above, we observe that the Triton kernel is approximately 4x faster than torch.jit. Feel free to modify some arguments to observe any differences.
In the next tutorial, we’ll demonstrate how to write a GEMM kernel with Triton and profile it using the Nsight system.