L2 regularization 和 weight decay

Posted on:November 5, 2021 at 12:00 AM

Table of contents

Open Table of contents

Introduction

通常我们在说 weight decay 的时候，都认为也是在说 L2 regularization，那么到底他们的实现是什么以及他们是否等价呢？这篇文章是一个简单的总结。

weight decay 和 L2 regularization 的原理

weight decay 的原理是在每次进行梯度更新的时候，额外再减去一个梯度，如果以普通的梯度下降为例，公式如下

θt+1=(θt−η∇(θt))−λθt=(1−λ)θt−η∇(θt)\theta_{t+1} = (\theta_{t} - \eta \nabla(\theta_t)) - \lambda \theta_t \\ = (1 - \lambda)\theta_{t} - \eta \nabla(\theta_t)

其中 λ\lambda 就是 weight decay 中设定的超参数，通常设定比较小。

L2 regularization 的原理是在计算 loss 的时候增加一个惩罚项，L2 即为增加一个二范数的惩罚项，即

freg(θt)=f(θt)+λ2∣∣θ∣∣22f^{reg}(\theta_t) = f(\theta_t) + \frac{\lambda}{2} ||\theta||_2^2

那么这时对参数求导并进行反向传播就可以有下面的公式

∂freg/∂θt=∂f/∂θt+λθt\partial f^{reg} / \partial \theta_t = \partial f / \partial \theta_t + \lambda \theta_t

那么再进行梯度更新的时候 L2 reg 就相当于额外减去 η×λ×θt\eta \times \lambda \times \theta_t，其中 η\eta 是学习率，λ\lambda 是 L2 reg 中设定的超参数

通过上面的公式可以看出 L2 reg 和 weight decay 虽然原理上不一致，不过通过推导在数学形式上最后只差一个常数倍，所以是否可以认为 L2 reg 和 weight decay 是等价的呢？

L2 reg 和 weight decay 等价吗？

通过上面的公式可以推导出 L2 reg 和 weight decay 是等价的，不过有一个大前提即上面的公式表达的是最普通的 SGD 更新方式，除了 vanilla SGD 之外，还有很多 variant optimizer 比如 SGDM，RMSprop，Adam 等等，下面我们以 Adam 为例再次进行 L2 reg 和 weight decay 的公式推导。

Adam 原理

首先回顾一下 Adam 的工作原理，给定超参 β1,β2\beta_1, \beta_2 以及学习率 η\eta，不考虑 L2 reg 和 weight decay 时，Adam 的更新公式如下

gt←∇ft(θt−1)mt←β1mt−1+(1−β1)gtvt←β2vt−1+(1−β2)gt2m^t←mt/(1−β1t)v^t←vt/(1−β2t)θt←θt−1−ηm^t/(v^t+ϵ)g_t \leftarrow \nabla f_t(\theta_{t-1}) \\ m_t \leftarrow \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t \leftarrow \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 \\ \hat{m}_t \leftarrow m_t / (1 - \beta_1^t) \\ \hat{v}_t \leftarrow v_t / (1 - \beta_2^t) \\ \theta_t \leftarrow \theta_{t-1} - \eta \hat{m}_t / (\sqrt{\hat{v}_t} + \epsilon)

Adam with weight decay and L2 reg

接下来可以在上面的公式中增加 L2 reg 和 weight decay，其中红色表示 L2 reg，绿色表示 weight decay

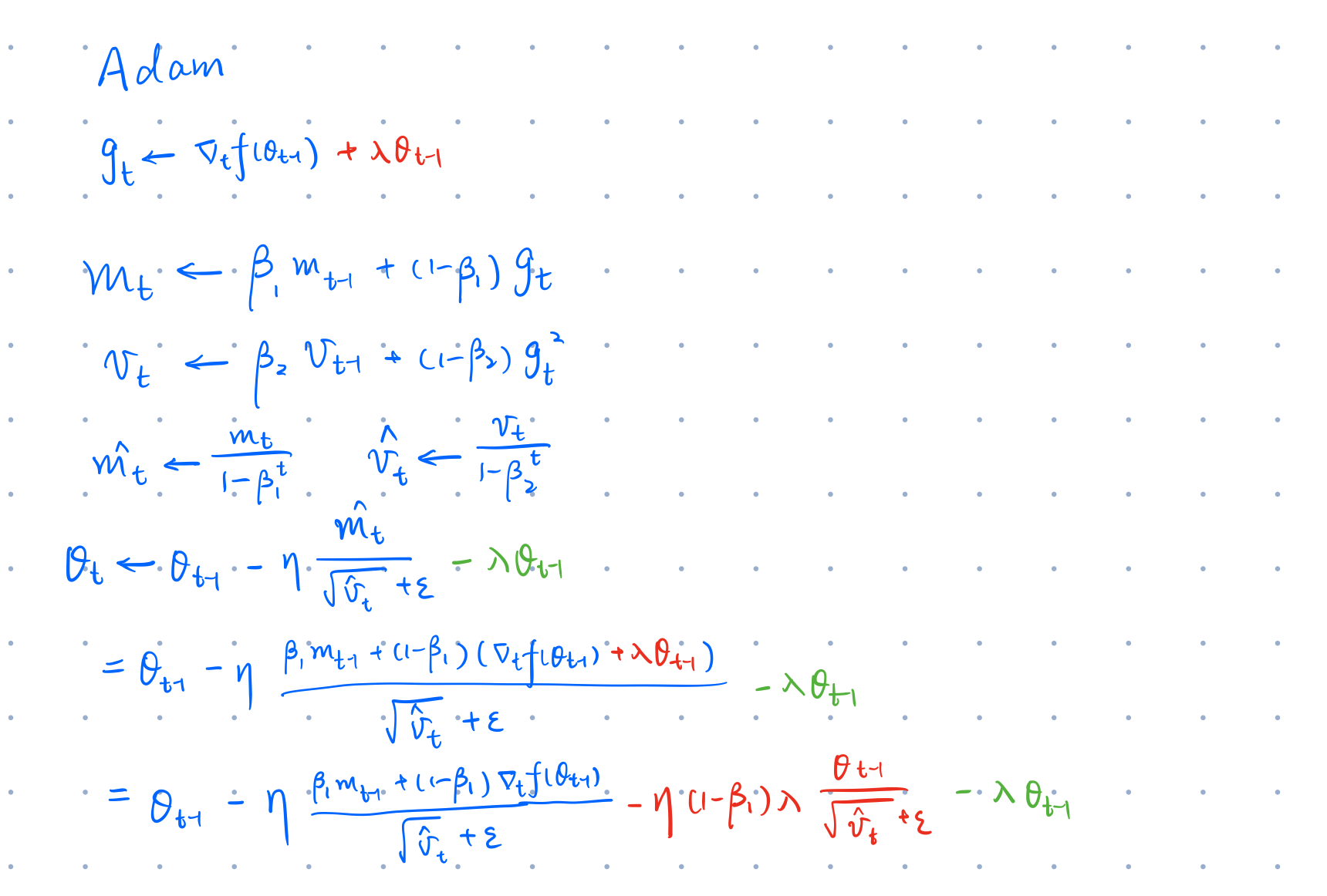
其中 m^t\hat{m}_t 是 bias correction，在 t 比较小的时候可以防止 mtm_t 因为初始值为 0 导致更新较少的问题，同时当 t→∞t \rightarrow \infty 时 m^t→mt\hat{m}_t \rightarrow m_t，所以在后续的公式中直接用 mtm_t 来代替 m^t\hat{m}_t

通过对公式的进一步展开和对比，可以发现 L2 reg 和 weight decay 之间除了有个常数倍 η(1−β1)\eta(1-\beta_1) 的区别外，一个更大的区别是 v^t\sqrt{\hat{v}_t} 作为分母，这里就引入了不一致性，因为当 grad 中某一个分量的值过大时，v^t\sqrt{\hat{v}_t} 就会变大，所以导致 l2 reg 作用在对应分量上的结果变小，这其实和 weight decay 的行为是不一致的，因为 weight decay 对所有的参数都应该是相同的惩罚项，所以正是因为自适应学习率等变种 optimizer 的出现导致 l2 reg 也进行了自适应，所以会导致和 weight decay 的结果最终不同。

当然因为 l2 reg 是作用了初始梯度上的，而一阶矩 mtm_t 和二阶矩 vtv_t 都需要依赖 gtg_t 进行更新，所以在不断的更新中也会导致他们在 l2 reg 和 weight decay 下的结果不一致，因为这里是一个积累差异，所以在公式中就没有详细展开了。

在这篇文章 ICLR19 的论文 DECOUPLED WEIGHT DECAY REGULARIZATION 中详细的进行了理论的推导和分析 l2 reg 和 weight decay 的差异以及最终的结果，最终为这种真正使用 weight decay 的 Adam 取名为 AdamW 作为区分，感兴趣的同学可以直接去阅读原文。

到底使用 Adam 还是 AdamW

之前大多数深度学习框架包括 TensorFlow 和 PyTorch 等都是按照 l2 reg 去实现的 Adam，不过要改为 AdamW 也比较简单，通过上面的分析是否说明我们应该把所有项目中使用的 Adam 都换成 AdamW 呢？

我的观点是之前项目中使用的 Adam 可以换成 AdamW 一试效果，如果精度较低就还是使用回 Adam，如果精度提升就换成 AdamW。那么为什么从上面的理论中得到 AdamW 才是正确的实现，但是实际使用 AdamW 也不一定好呢？原因有很多，因为深度神经网络是一个黑盒，没有人能详细的计算出内部的运算原理，同时之前调参和各种 tricks 都是基于 Adam 去做的，已经针对 Adam+l2 reg 的进行了比较细致的优化，这时直接换成 AdamW 可能重新做一些调参工作可以超过之前的结果，不过就不建议去做重复劳动了。

在新项目中可以直接使用 AdamW，同时基于 AdamW 进行调参，这样可以尽可能保证得到更好的结果，比如 Bert 就直接使用的 AdamW。

Ending

最后希望这篇文章能够让你了解 l2 reg 和 weight decay 之间的区别和联系，如果你有任何建议和问题欢迎在评论去留言，希望这篇文章能够帮助到你们。

Reference

Comments