GPTQ Code Implementation

Posted on:September 18, 2023 at 12:00 AM

This blog post delves into the nuts and bolts of implementing GPTQ, focusing on the quantization of a Llama model as our primary example. The implementation process is guided by the GPTQ-triton GitHub repository.

If you’re not yet acquainted with the underlying algorithm of GPTQ, I recommend starting with my previous blog post on GPTQ Math Derivation.

Table of Contents

Open Table of Contents

Building the Model

The first step in our journey is to construct the model we wish to quantize. Given that GPTQ is a universal quantization algorithm, it is agnostic to the specific architecture of the model. Therefore, control over model construction should be left to the users.

The transformers library has become the go-to resource for pre-trained models, and Llama is among its most popular offerings. For this walkthrough, we’ll use Llama as our example to demonstrate the GPTQ implementation process.

Interestingly, you can use the default model-building steps provided by the transformers library without any modifications to accommodate GPTQ. However, it’s worth noting that model initialization can be both meaningless and resource-intensive, especially when we plan to use pre-trained weights.

To speed up the model-building process, you can use the following Python code snippet:

def skip(*args, **kwargs):
    pass

# NOTE: This is a nasty hack, but it speeds up model building by a huge amount
torch.nn.init.kaiming_uniform_ = skip
torch.nn.init.uniform_ = skip
torch.nn.init.normal_ = skip

Once the model is initialized, setting up the tokenizer is straightforward and can be done using AutoTokenizer.from_pretrained.

Building the DataLoader

Once the model and tokenizer are set up, the next step is to prepare the calibration data. This data serves to simulate real-world distribution and is crucial for the GPTQ algorithm, which is a one-shot method. In other words, GPTQ uses this calibration data to quantize the model’s floating-point weights into integers.

In the GPTQ-triton repository, you have the option to choose from four public datasets: 'wikitext-2', 'ptb', 'ptb-new', 'c4'. However, the flexibility of GPTQ allows you to easily incorporate your own custom datasets, much like you would during the training phase.

In addition to selecting a calibration dataset, you’ll also need to decide on the number of samples (nsamples) and the sequence length (seq_len) that best suit your specific use case.

Quantization Process

After completing the prerequisites, we arrive at the quantization step. The entire process comprises the following five steps:

  1. Optimize GPU Memory Usage: Move each transformer_layer in the model to the GPU one by one. This significantly reduces GPU DRAM usage, which is crucial when quantizing very large models.
  2. Forward Pass: Before proceeding with the quantization of a transformer_layer, execute a forward pass to gather the necessary information.
  3. Layer-wise Quantization: Quantize each nn.Linear layer within the transformer_layer using GPTQ. In the Llama model, these layers are as follows: 
    ['self_attn.k_proj', 'self_attn.v_proj', 'self_attn.q_proj'],
['self_attn.o_proj'],
['mlp.up_proj', 'mlp.gate_proj'],
['mlp.down_proj']
  4. QuantLinear: Replace all instances of nn.Linear in the model with QuantLinear. This is a custom kernel designed to fuse dequantization and computation.
  5. Weight Pack: Pack the quantized weights into QuantLinear for use in step 4 and save the model.

Next, we will explain the core steps in the above procedure.

Llama Sequential

This section covers steps 1-3 of the process.

Catcher

To obtain the attention_mask and position_ids, we can create a dummy layer that serves as a “catcher” for these input parameters. The specific code for this is as follows:

cache = {'i': 0, 'attention_mask': None, 'position_ids': None}
class Catcher(nn.Module):
    def __init__(self, module):
        super().__init__()
        self.module = module

    def forward(self, inp, **kwargs):
        inps[cache['i']] = inp
        cache['i'] += 1
        if cache['attention_mask'] is not None:
            assert torch.all(cache['attention_mask'] == kwargs['attention_mask'])
        cache['attention_mask'] = kwargs['attention_mask']
        if cache['position_ids'] is not None:
            assert torch.all(cache['position_ids'] == kwargs['position_ids'])
        cache['position_ids'] = kwargs['position_ids']
        raise ValueError

layers[0] = Catcher(layers[0])
for batch in dataloader:
    try:
        model(batch.to(device))
    except ValueError:
        pass
layers[0] = layers[0].module

Simply wrap the first layer in the Catcher and feed it the input to gather all the necessary information. Once this is done, revert the module back to its original state.

Forward Order

When it comes to quantizing each layer, you have the option to enable the true_sequential mode. If enabled, GPTQ will quantize each nn.Linear layer in the order they execute during the model’s forward pass.

if true_sequential:
    sequential = [
        ['self_attn.k_proj', 'self_attn.v_proj', 'self_attn.q_proj'],
        ['self_attn.o_proj'],
        ['mlp.up_proj', 'mlp.gate_proj'],
        ['mlp.down_proj']
    ]
else:
    sequential = [list(full.keys())]

This part should be abstracted to allow for customization with other models.

Add Batch

Before running GPTQ on a given nn.Linear layer, we can precompute the Hessian matrix by utilizing the inputs. This is where PyTorch’s hook functionality comes in handy. By registering a forward_hook in each nn.Linear layer, the hook will execute immediately after the module’s forward method. Within this custom hook function, we can compute the Hessian matrix.

Additionally, the output can be saved for further debugging, error analysis and subsequent layers use.

# Feed data to the quantizer, and save outs
def add_batch(name):
    def tmp(_, inp, out):
        gptq[name].add_batch(inp[0].data, out.data)
    return tmp

handles = []
for name in subset:
    handles.append(subset[name].register_forward_hook(add_batch(name)))

For GPTQ.add_batch, the specific code as follows:

def __init__(self, layer):
...
    self.rows = W.shape[0]
    self.columns = W.shape[1]
    self.H = torch.zeros((self.columns, self.columns), device=self.dev)
    self.nsamples = 0
...
def add_batch(self, inp, out):
    self.H *= self.nsamples / (self.nsamples + tmp)
    self.nsamples += tmp
    inp = math.sqrt(2 / self.nsamples) * inp.float()
    self.H += inp.matmul(inp.t())

Hessian Matrix

The primary function of add_batch is to compute the Hessian matrix. In the code mentioned earlier, self.H represents the Hessian matrix of the weight W, and its shape is (col, col).

In the nn.Linear layer, the computation is expressed as y=xW^T + b. If the shape of x is (batch*seq, inp_dim), then the shape of W is (out_dim, inp_dim). The quantization process operates row-wise along out_dim. For each row of W, the shape of the Hessian matrix is (inp_dim, inp_dim) which corresponding to the col of W.

Recall the formula for the error introduced by quantization:

E=arg min⁡W^∣∣WX−W^X∣∣2E = \argmin_{\hat{\mathbf{W}}} ||\textbf{W} \textbf{X} - \hat{\textbf{W}} \textbf{X}||^2

Upon observation, we find that the Hessian matrix H\mathbf{H} for each row of W\mathbf{W} is 2XX2\mathbf{X}\mathbf{X}. This Hessian matrix can be reused for all subsequent computations.

The Hessian matrix is computed in add_batch. Specifically, the function calculates the average value of the Hessian matrix across all calibration data. The update process can be derived as follows: Given the average Hessian matrix Hk−1\mathbf{H}_{k-1} for k-1 samples, the Hessian matrix Hk\mathbf{H}_k for k samples can be updated as:

Hk−1⇒HkHk=Hk−1⋅(k−1)+2(inpk⊤⋅inpk)k=k−1k⋅Hk−1+2k(inpk⊤⋅inpk)\begin{aligned} \mathbf{H}_{k-1} & \Rightarrow \mathbf{H}_k \\ \mathbf{H}_k & =\frac{\mathbf{H}_{k-1} \cdot(k-1)+2\left(\text{inp}_k^{\top} \cdot \text{inp}_k\right)}{k} \\ & =\frac{k-1}{k} \cdot \mathbf{H}_{k-1}+\frac{2}{k}\left(\text{inp}_k^{\top} \cdot \text{inp}_k\right) \end{aligned}

According to this formula, H is multiplied by k−1k\frac{k-1}{k}, and the input is multiplied by 2k\sqrt{\frac{2}{k}}.

Diagonal Processing

The diagonal elements of the Hessian matrix represent the sum of squares of each feature across all samples, as Hi,i=∑j=0nXj[i]2H_{i,i} = \sum_{j=0}^n X_j[i]^2.

Firstly, we address the zero values in the diagonal. If a diagonal element is zero, it implies that the corresponding feature across all samples is zero. In such cases, we can safely set the corresponding weight to zero as well.

dead = torch.diag(H) == 0
H[dead, dead] = 1
W[:, dead] = 0

Next, we have the option to sort the diagonal elements and their corresponding weights. The underlying assumption here is that the larger the diagonal element, the more important the corresponding weight is. By sorting, we can prioritize quantizing the more important weights first, followed by the less important ones.

if actorder:
    perm = torch.argsort(torch.diag(H), descending=True)
    W = W[:, perm]
    H = H[perm][:, perm]

This sorting step is optional but can be beneficial when you want to focus on preserving the most important features during the quantization process.

Inverse of the Hessian Matrix

To expedite the quantization process, it’s advantageous to compute the inverse of the Hessian matrix beforehand. However, numerical stability can be a concern when inverting the matrix.

The GPTQ paper suggests two approaches to address this issue. The first one involves dampening, where a small constant λ\lambda is added to the diagonal elements of H\mathbf{H}. A recommended value for λ\lambda is 1% of the average diagonal value.

damp = percdamp * torch.mean(torch.diag(H))
diag = torch.arange(self.columns, device=self.dev)
H[diag, diag] += damp

The second approach employs Cholesky decomposition1 to compute the inverse of H\mathbf{H}. By doing so, we can extract all the necessary information from the resulting upper triangular matrix for later use.

# compute inv(H) using Cholesky Decomposition
L = torch.linalg.cholesky(H)
Hinv = torch.cholesky_inverse(L)
# Hinv <- Cholesky(Hinv).T in Algorithm 1
Hinv = torch.linalg.cholesky(Hinv, upper=True)

Both methods aim to ensure numerical stability while providing an efficient way to compute the inverse of the Hessian matrix, which is crucial for the subsequent quantization steps.

The GPTQ Algorithm

In the original OBQ algorithm, a greedy order is employed to quantize each row individually. This approach necessitates maintaining a distinct Hessian matrix for each row due to the varying quantization order. However, GPTQ simplifies this by quantizing all rows in the same order, allowing for the use of a single, shared Hessian matrix. Importantly, this matrix doesn’t require updating during the process, as the order of quantization is consistent across rows and doesn’t depend on previously quantized columns.

GPTQ operates in a block-wise manner, iterating through blocks of columns to strike a balance between computational efficiency and memory access. Within each block, the algorithm iterates through individual columns, quantizing each one and then updating the remaining weights to minimize the introduced errors.

Additionally, the groupsize parameter can be set to divide the columns into multiple groups, with the default being a single group. This allows for more nuanced quantization, providing an extra layer of customization to the process.

for i1 in range(0, self.columns, blocksize):
    i2 = min(i1 + blocksize, self.columns)
    count = i2 - i1

    W1 = W[:, i1:i2].clone()
    Q1 = torch.zeros_like(W1)
    Err1 = torch.zeros_like(W1)
    Losses1 = torch.zeros_like(W1)
    Hinv1 = Hinv[i1:i2, i1:i2]

    # for j = i, i+1, ..., i+B-1
    for i in range(count):
        w = W1[:, i]
        d = Hinv1[i, i]

        if groupsize != -1:
            if (i1 + i) % groupsize == 0:
                self.quantizer.find_params(W[:, (i1 + i):(i1 + i + groupsize)], weight=True)

            if ((i1 + i) // groupsize) - now_idx == -1:
                scale.append(self.quantizer.scale)
                zero.append(self.quantizer.zero)
                now_idx += 1

        q = quantize(
            w.unsqueeze(1), self.quantizer.scale, self.quantizer.zero, self.quantizer.maxq
        ).flatten()
        Q1[:, i] = q
        Losses1[:, i] = (w - q) ** 2 / d ** 2

        err1 = (w - q) / d
        W1[:, i:] -= err1.unsqueeze(1).matmul(Hinv1[i, i:].unsqueeze(0))
        Err1[:, i] = err1

    Q[:, i1:i2] = Q1
    Losses[:, i1:i2] = Losses1 / 2

    W[:, i2:] -= Err1.matmul(Hinv[i1:i2, i2:])

The quantize function serves as a simulation tool for the quantization and dequantization processes.

def quantize(x, scale, zero, maxq):
    if maxq < 0:
        return (x > scale / 2).float() * scale + (x < zero / 2).float() * zero
    q = torch.clamp(torch.round(x / scale) + zero, 0, maxq)
    return scale * (q - zero)

It’s necessary to dequantize the quantized weights back to fp16 format in kernel computation. This is because using integer weights in matrix multiplication could lead to overflow issues in LLM2. By employing this quantize function, we can effectively gauge the discrepancies between the dequantized weights and their original floating-point counterparts.

Quantizer

The Quantizer class is responsible for calculating the scale and zero-point values for the weights W. Initialization and configuration of quantization-related parameters occur in the __init__ and configure methods. These parameters include options for symmetric or asymmetric quantization, the number of bits used for quantization, and so on.

It’s important to note the dual role of the self.zeros attribute. In the context of asymmetric quantization, self.zeros serves as the zero-point. However, in symmetric quantization, it defines the range of quantized values. For instance, if self.zero is set to 8 in a 4-bit symmetric quantization, the range of quantized values will span from -8 to 7.

def __init__(self, shape=1):
    super(Quantizer, self).__init__()
    self.register_buffer('maxq', torch.tensor(0))
    self.register_buffer('scale', torch.zeros(shape))
    self.register_buffer('zero', torch.zeros(shape))

def configure(
    self,
    bits, perchannel=False, sym=True,
    mse=False, norm=2.4, grid=100, maxshrink=.8,
    trits=False
    ):

    self.maxq = torch.tensor(2 ** bits - 1)
    self.perchannel = perchannel
    self.sym = sym
    self.mse = mse
    self.norm = norm
    self.grid = grid
    self.maxshrink = maxshrink
    if trits:
        self.maxq = torch.tensor(-1)

The find_params function is where the scale and zero-point values are computed.

tmp = torch.zeros(x.shape[0], device=dev)
xmin = torch.minimum(x.min(1)[0], tmp)
xmax = torch.maximum(x.max(1)[0], tmp)

if self.sym:
    xmax = torch.maximum(torch.abs(xmin), xmax)
    tmp = xmin < 0
    if torch.any(tmp):
        xmin[tmp] = -xmax[tmp]
tmp = (xmin == 0) & (xmax == 0)
xmin[tmp] = -1
xmax[tmp] = +1

self.scale = (xmax - xmin) / self.maxq
if self.sym:
    self.zero = torch.full_like(self.scale, (self.maxq + 1) / 2)
else:
    self.zero = torch.round(-xmin / self.scale)

Finally, the function also includes a grid search strategy to find the optimal number of bits for each row, aiming to minimize quantization errors. This is particularly useful for a finer quantization.

Llama Pack

This section covers steps 4 and 5 of the quantization process, focusing on how to efficiently store and substitute the original weights with their quantized counterparts.

QuantLinear Substitution

The first step is to replace all instances of nn.Linear in the model with QuantLinear. This is straightforward and can be accomplished by iterating through all the modules in the model. However, it’s important to note that we do not replace the lm_heads module. This ensures that the language model’s output layer remains unchanged, preserving its original functionality.

def make_quant(model, bits, groupsize):
    """
    Replace all linear layers in a model with quantized ones.
    Except for the lm_head, which is not quantized.
    """
    for name, m in model.named_modules():
        if not isinstance(m, nn.Linear):
            continue

        if name == 'lm_head':
            continue

        # Replace the linear layer with a quantized one
        qlayer = QuantLinear(bits, groupsize, m.in_features, m.out_features, m.bias is not None)
        parent_name = name.rsplit('.', 1)[0]
        parent = model.get_submodule(parent_name)
        setattr(parent, name[len(parent_name) + 1:], qlayer)

Packing Weights

The next step involves efficiently storing three types of data: the quantized weights Q, and the quantization parameters - scale and zeros.

The scale is stored as a 16-bit floating-point number (fp16). This is straightforward and doesn’t require any special handling.

Storing Q and zeros requires a more strategic approach. Since Q consists of fixed-point numbers, we can combine multiple elements into a single storage one. This allows us to read a single element from memory but parse multiple quantized weights from it.

# Round weights to nearest integer based on scale and zero point
# Each weight will be one int, but should not exceed quant.bits
intweight = []
for idx in range(quant.infeatures):
    g_idx = idx // quant.groupsize
    q = torch.round((weights[:,idx] + scale_zeros[g_idx]) / scales[g_idx]).to(torch.int32)
    intweight.append(q[:,None])
intweight = torch.cat(intweight,dim=1)
intweight = intweight.t().contiguous()

After obtaining the quantized weights Q, we can further optimize storage by using bitwise operations3. The idea is to pack multiple quantized weight elements into a single integer, taking advantage of the fixed bit-width of the quantized values.

For instance, if we’re using 8-bit quantization, a uint32 data type can hold four 8-bit quantized elements. This is because uint32 has 32 bits, and each 8-bit quantized element would occupy one-fourth of that space.

The key operation here is quant.qweight[row] |= intweight[j] << (quant.bits * (j - i)). In this expression:

This operation effectively packs four 8-bit quantized elements into a single uint32 integer, thereby reducing the storage requirements and potentially speeding up memory access during model inference.

quant.qweight.zero_()
i = 0
row = 0
while row < quant.qweight.shape[0]:
    if quant.bits in [2,4,8]:
        for j in range(i, i + (32 // quant.bits)):
            quant.qweight[row] |= intweight[j] << (quant.bits * (j - i))
        i += 32 // quant.bits
        row += 1
    else:
        raise NotImplementedError("Only 2,4,8 bits are supported.")

To illustrate the bitwise packing process, consider the following example where we pack the first four rows of intweight into the first row of qweight.

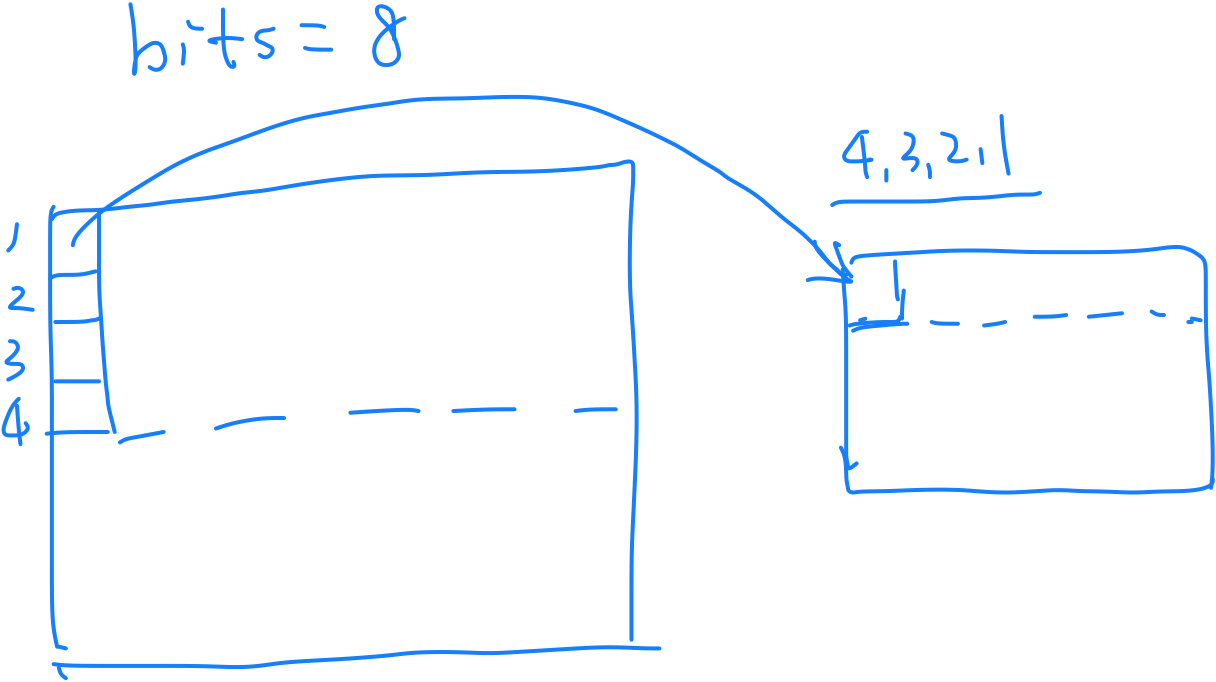
Pack Zero

The process for packing the zero points (qzeros) is similar to that of packing the quantized weights (qweight).

# Subtract 1 from the zero point
zeros = zeros - 1

# Pack the zero points into uint32's
zeros = zeros.to(torch.int32)
quant.qzeros.zero_()
i = 0
col = 0
while col < quant.qzeros.shape[1]:
	if quant.bits in [2,4,8]:
		for j in range(i, i + (32 // quant.bits)):
			quant.qzeros[:, col] |= zeros[:, j] << (quant.bits * (j - i))
		i += 32 // quant.bits
		col += 1
	else:
		raise NotImplementedError("Only 2,4,8 bits are supported.")

Summary

In this blog post, we’ve delved into the code implementation of the GPTQ quantization process, using the Llama model as a case study. It’s worth noting that GPTQ is a model-agnostic method, making it applicable to a wide range of model architectures. We hope this deep dive has enhanced your understanding of GPTQ and its practical applications.

Thank you for reading!

Reference

Footnotes

  1. https://en.wikipedia.org/wiki/Cholesky_decomposition ↩

  2. https://timdettmers.com/2022/08/17/llm-int8-and-emergent-features/ ↩

  3. https://en.wikipedia.org/wiki/Bitwise_operation ↩

Comments